概率论基础
概率论基础
随机试验: 事先不能完全预知其结果的试验.
样本空间: 随机试验的所有可能结果组成的集合, 记为 \(\Omega\).
原子事件: 样本空间中的点, 即随机试验的可能结果, 记为 \(\omega\).
事件: 样本空间的子集, 记为 \(A, B, \ldots\). \(\Omega\) 为必然事件, \(\emptyset\) 为不可能事件.
互斥事件: \(A \cap B = \emptyset\).
互补事件: \(A \cap B = \emptyset\) 且 \(A \cup B = \Omega\).
概率测度: 给样本空间中的每一个事件赋予一个数值(概率), \(P(A) \in [0,1]\).
对于样本空间 \(\Omega\) 来说, 包含的事件总数为 \(2^{\Omega}\) 个. 概率测试表示的是所有事件到区间 \([0,1]\) 的一个映射. 并且满足以下公理:
- \(P(\Omega) = 1\) (规范性)
- \(P(A) \geq 0, \forall A \in 2^{\Omega}\) (非负性)
- \(P(A \cup B) = P(A) + P(B), \forall A, B \in 2^{\Omega}, A \cap B = \emptyset\) (有限可加性)
\(P(A)\) 称为事件 \(A\) 的概率.
随机变量: 定义在样本空间 \(\Omega\) 上的函数, 记为 \(X, Y, Z\).
随机变量的取值随试验结果而定, 记为 \(x, y, z\).
状态空间: 随机变量 \(X\) 的所有可能取值的集合, 记为 \(\Omega_x\).
= \(X=x\) =: 设 \(X\) 为一随机变量, \(x\) 是它的一个取值, 在样本空间 \(\Omega\) 中, 所有使 \(X\) 取值为 \(x\) 的原子事件组成一个事件, 记为 \(\Omega_{X=x} = {\omega \in \Omega} \mid X(\omega) = x\), 简记为 \(X=x\).
= $P(X) $=: 事件 \(X=x\) 的概率 \(P(X=x) = P(\Omega_{X=x})\) 依赖于 \(X\) 的取值 \(x\), 让 \(x\) 在 \(\Omega_X\) 上变动, \(P(X=x)\) 就称为 \(\Omega_X\) 的一个取值在 \([0,1]\) 之间的函数, 称为随机变量 \(X\) 的概率质量函数, 记为 \(P(X)\).
联合概率
如 \(P(X_1, X_2)\), 包含多个条件,且所有条件同时成立
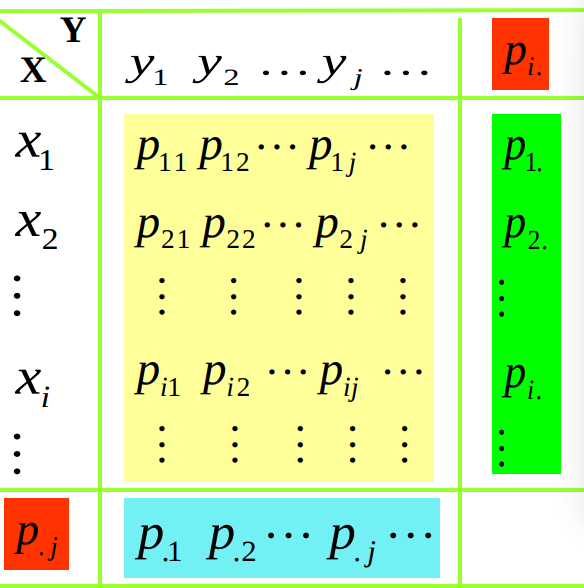
联合分布通常表示为一张表, 如下所示:
边缘概率
仅与单个随机变量有关
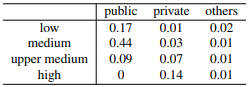
直接举个离散型随机变量的边缘分布:
条件概率
如 \(P(A \mid B) = \frac{P(A \cap B)}{P(B)}\), B发生的前提下,A发生的概率
条件概率分布
\(P(X=x \mid Y=y) = \frac{P(X=x, Y=y)}{P(Y=y)}\)
条件独立
事件 \(A, B\) 相互独立, 则: \(P(A, B) = P(A)(B)\)
链规则
如果随机变量之间相互独立, 则有:
\(P(X_1, X_2, \ldots, X_n) = P(X_1)P(X_2 \mid X_1) \ldots P(X_n \mid X_1, \ldots, X_{n-1})\)
贝叶斯定理
设 \(H\) 和 \(E\) 是两个随机变量, \(H=h\) 为某一假设, \(E=e\) 为一组证据。在考虑 \(E=e\) 之前, \(P(H=h)\) 为先验概率,考虑 \(E=e\) 之后, \(P(H=h \mid E=e)\) 为后验概率。
贝叶斯定理描述了先验概率和后验概率之间的关系:
$$P(H=h \mid E=e)=\frac{P(H=h)P(E=e \mid H=h)}{P(E=e)}$$
这也称为贝叶斯公式。
Generated by Emacs 25.x(Org mode 8.x)
Copyright © 2014 - Pinvon - Powered by EGO
