贝叶斯网

概述
不确定性推理与联合概率分布
- 传统的使用概率方法进行不确定性推理
  - 例子
条件独立与联合分布的分解
- 使用条件独立降低复杂度
贝叶斯网的概念
- 贝叶斯网的构造
  - 确定网络结构
- 确定网络参数
图分隔与变量独立
周志华-机器学习-贝叶斯网
贝叶斯网推理
- 近似推理
  - 吉布斯采样
  - EM算法

概述

贝叶斯网: 一种帮助人们将概率统计应用于复杂领域, 进行不确定性推理和数值分析的工具. 它是概率论和图论结合的产物, 一方面用图论的语言直观揭示问题的结构, 另一方面用概率论的原则对问题结构加以利用.

贝叶斯网学习: 从数据出发, 获得贝叶斯网的过程.

不确定性推理与联合概率分布

不确定性推理是人工智能研究的重要课题之一。有概率方法、非单调逻辑、确定因子、DS证据理论、模糊逻辑等方法。

传统的使用概率方法进行不确定性推理

把问题用一组随机变量 $X={X_1, X_2, \ldots, X_n}$ 来刻画
把关于问题的知识表示为一个联合概率分布 $P(X)$
按照概率论原则进行推理计算

例子

Pearl教授家住在洛杉矶，地震和盗窃时常发生，教授家里装有警铃，地震和盗窃都有可能触发警铃。听到警铃后，两个邻居Mary和John可能会打电话给他。一天，教授接到Mary的电话，问他家被盗窃的概率。

问题里包含5个变量：盗窃( $B$ )、地震( $E$ )、警铃响( $A$ )、接到John的电话( $J$ )和接到Mary的电话( $M$ )；所有变量取值为 $y$ 或 $n$ 。这些变量间的关系存在不确定性：盗窃和地震以一定概率发生；它们发生后，以一定概率触发警铃；警铃响后，Mary和John只有一定概率听到。

要计算的是接到Mary的电话 $(M=y)$ 后，教授家被盗 $(B=y)$ 的信度（贝叶斯理论中的概率，与频率方法的概率，是不一样的），也就是计 $P(B=y \mid M=y)$

先计算边缘分布， $P(B,M) = \sum_{E,A,J}P(B,E,A,J,M)$

再根据条件概率，得 $P(B=y \mid M=y) = \frac{P(B=y, M=y)}{P(M=y)} = \frac{P(B=y, M=y)}{P(B=y,M=y) + P(B=n,M=y)}$

但是这种方法，复杂度较高，因为要计算边缘分布，首先要得到联合分布，而联合分布的计算复杂度极高，在上例中，只有5个二值随机变量，就包含 $2^5-1=31$ 个独立参数。联合分布的复杂度相对于变量的个数，成指数增长。

条件独立与联合分布的分解

使用链规则，例子中的联合概率分布又可以表示为： $$P(B,E,A,J,M)=P(B)P(E \mid B)P(A \mid B,E)P(J \mid B,E,A)P(M \mid B,E,A,J)$$

虽然这一步并没有降低模型的复杂度，因为等式右端的5个概率分布，仍然包含同联合分布相同个数的独立参数： $1+2+4+8+16=31$ 。但是根据问题的背景知识，做一些合理的独立假设，则可以降低复杂度。如假设 $E$ 与 $B$ 无关，则 $P(E \mid B)=P(E)$ ，另外， $M,J,B,E$ 都相互独立，因此，最后可得： $$P(B,E,A,J,M)=P(B)P(E)P(A \mid B,E)P(J \mid A)P(M \mid A)$$

这样，等式右端的概率分布仅包含 $1+1+4+2+2=10$ 个独立参数。

使用条件独立降低复杂度

一个包含 $n$ 个变量的联合分布 $P(X_1, \ldots, X_n)$ ，可以根据链规则，写成： $$P(X_1, \ldots, X_n)=P(X_1)P(X_2 \mid X_1) \cdots P(X_n \mid X_1,X_2, \dots,X_{n-1})= \prod^{n}_{i=1}P(X_i \mid X_1, X_2, \cdots, X_{i-1})$$

对于任意 $X_i$ ，如果存在 $\pi(X_i) \subseteq {X_1, \cdots, X_{i-1}}$, 使得 $X_i$ 与除 $\pi(X_i)$ 之外的变量条件独立。即： $$P(X_i \mid X_1, \cdots, X_{i-1}) = P(X_i \mid \pi(X_i))$$

则有： $$P(X_1, \cdots, X_n) = \prod^{n}_{i-1}P(X_i \mid \pi(X_i))$$

这样，对于任意的 $X_i$ ，$\pi(X_i)$ 最多包含 $m$ 个变量。如果所有变量取二值时，独立参数最多为 $n2^m$ 个。因此，条件独立使模型得到了简化。

贝叶斯网的概念

构造有向图来表示变量之间的依赖和独立关系：

把每个变量都表示为一个节点
对于每个节点 $X_i$ ，都从 $\pi(X_i)$ 中的每个节点画一条有向边到 $X_i$

如警铃那个例子， $A$ 依赖于 $B,E$ ， $M,J$ 依赖于 $A$ 。构造的有向图如下所示：

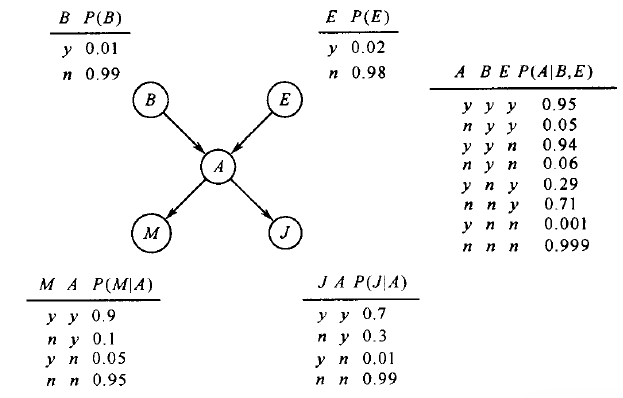
Figure 1: Alarm贝叶斯网

贝叶斯网是一个有向无环图，其中节点代表随机变量，节点间的边代表变量之间的直接依赖关系。 每个节点都附有一个概率分布 。根节点所附的是边缘分布 $P(X)$ ，非根节点所附的是条件概率分布 $P(X \mid \pi(X))$ .如果把各变量所附的概率相乘，就得到联合分布。即： $$P(X_1, \cdots, X_n) = \prod^{n}_{i-1}P(X_i \mid \pi(X_i))$$

贝叶斯网的构造

确定网络结构

选定一组刻画问题的随机变量 ${X_1, X_2, \ldots, X_n}$
选择一个变量顺序 $\alpha = \langle X_1, X_2, \ldots, X_n \rangle$
从一个空图出发, 按照顺序将 $\alpha$ 逐个将变量加入 $\delta$ 中
在加入变量 $X_i$ 时, $\delta$ 中的变量包括 $X_1, X_2, \ldots, X_{i-1}$. 利用背景知识, 在这些变量中选择一个尽可能小的子集 $\pi(X_i)$, 使得假设"给定 $\pi(X_i)$, $X_i$ 与 $\delta$ 中的其他变量条件独立"合理; 从 $\pi(X_i)$ 中的每一个节点添加一条指向 $X_i$ 的有向边.
不同的变量顺序导致不同的网络结构, 不同的网络结构表示了联合分布的不同分解, 而不同的分解则意味着不同的复杂度
建议用因果关系来决定变量顺序, 原因在前, 结果在后

确定网络参数

贝叶斯网的参数就是各变量的概率分布。由于参数的确定一般依靠专家，耗费人力和时间，因此要尽量减少参数的个数。

如果变量 $Y$ 有 $m$ 个父节点 $X_1, \cdots, X_m$ ，则 $Y$ 对父节点的依赖关系为 $P(Y \mid X_1, \cdots, X_m)$ 。当所有变量均取二值时，有 $2^m$ 个独立参数。

减少参数个数的方法有因果机制独立和环境独立。

图分隔与变量独立

概述

贝叶斯网是概率论和图论相结合的产物. 可以从概率论的角度讨论变量间的依赖与独立, 也可以从图论的角度讨论节点间的连通与分隔, 这两者之间有着深刻的联系.

通过图论准则, 可以判别变量之间条件独立关系.

$X$ 与 $Y$ 不直接相连, 通过其他变量才勇夺两者之间传递信息, 如果 $X$ 与 $Y$ 之间的所有信息通道都被阻塞, 则信息就无法继续传递.

图分隔与变量独立

变量 $X$ 与 $Y$ 通过第三个变量 $Z$ 间接相连的三个情况:

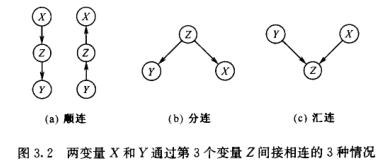
阻塞

设 $\mathbf{Z}$ 为节点集合, $X$ 和 $Y$ 是不在 $\mathbf{Z}$ 中的两个节点, 考虑 $X$ 和 $Y$ 之间的一条通道 $\alpha$, 如果满足以下任意一个条件, 则称 $\alpha$ 被 $\mathbf{Z}$ 阻塞:

$\alpha$ 上有一个在 $\mathbf{Z}$ 中的顺连节点
$\alpha$ 上有一个在 $\mathbf{Z}$ 中的分连节点
$\alpha$ 上有一个汇连节点 $W$, 它和它的后代节点均不在 $\mathbf{Z}$ 中

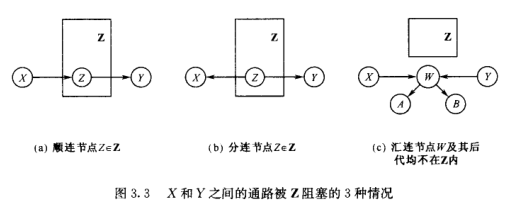
如果 $X$ 和 $Y$ 之间的所有通路都被 $\mathbf{Z}$ 阻塞, 则我们称: $\mathbf{Z}$ 有向分隔(directed separate) $X$ 和 $Y$, 简称 d-separate.

整体马尔科夫性: 设 $X$ 和 $Y$ 是贝叶斯网 $\mathcal{N}$ 中的两个变量, $mathbf{Z}$ 为 $\mathcal{N}$ 中一个不包含 $X$ 和 $Y$ 的节点集合. 如果 $\mathbf{Z}$ d-separate $X$ 和 $Y$, 那么 $X$ 和 $Y$ 在给定 $\mathbf{Z}$ 时条件独立.

d-separate 是图论的概念, 而条件独立是概率论的概念, 所以 整体马尔科夫性 定理提示了贝叶斯网络图论侧面和概率论侧面之间的关系.

马尔科夫边界与端正图

马尔科夫性: 在一个随机过程中, 如果事件发生概率在 $t$ 时刻所处的状态已知, 它在 $t+1$ 时刻的状态只与 $t$ 时刻的状态有关, 而与其他的状态无关, 则称该过程具有马尔科夫性.

马尔科夫边界: 在贝叶斯网络中, 一个节点 $X$ 的马尔科夫边界包括其父节点, 子节点, 以及子节点的父节点.

在一个贝叶斯网络中, 给定变量 $X$ 的马尔科夫边界 $mb(X)$, 则 $X$ 条件独立于网络中所有其他变量.

周志华-机器学习-贝叶斯网

一个贝叶斯网 $B$ 由结构 $G$ 和参数 $\Theta$ 两部分构成, 即 $B=\langle G,\Theta \rangle$. 其中, 网络结构 $G$ 是一个有向无环图, 其每个结点对应一个属性, 如果两个属性有直接依赖关系, 则它们由一条边连接起来; 参数 $\Theta$ 定量描述这种依赖关系. 假设属性 $x_i$ 在 $G$ 中的父结点集为 $\pi_i$, 则 $\Theta$ 包含了每个属性的条件概率表 $\theta_{x_i \mid \pi_i} = P_{B}(x_i \mid \pi_i)$.

贝叶斯网假设每个属性与它的非直接相连属性是相互独立的. 所以 $B=\langle G, \Theta \rangle$ 将属性 $x_1, x_2, \ldots, x_d$ 的联合概率分布定义为:

$$P_B(x_1, x_2, \ldots, x_d) = \Pi_{i=1}^{d}P_B(x_i \mid \pi_i) = \Pi_{i=1}^{d} \theta_{x_i \mid \pi_i}$$

例子

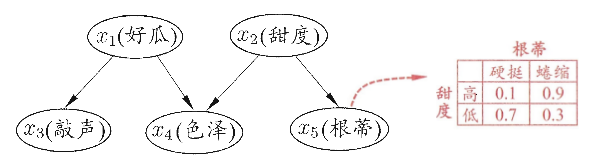
图中, 这些节点的联合概率分布为:

$$P(x_1, x_2, x_3, x_4, x_5) = P(x_1)P(x_2)P(x_3 \mid x_1)P(x_4 \mid x_1, x_2)P(x_5 \mid x_2)$$

d-separation(有向分离)

这边再提一次 d-separation. 前面看的是 <贝叶斯网引论>, 这边看的是周志华老师写的 <机器学习>, 感觉比较好懂.

通过 d-separation, 可以将一个有向图变为一个无向图. 做法如下:

找出有向图中所有汇连结构, 把汇连结构中的两个父结点用一条无向边连接起来.
把所有有向边改成无向边.

贝叶斯网的学习

如果网络结构已知, 即属性间的依赖关系已知, 则贝叶斯网的学习过程比较简单, 只需要通过对训练样本"计数", 估计出每个结点的条件概率表即可.

在实际应用中, 往往不知道网络结构, 所以贝叶斯网的学习, 首先要根据训练数据找出结构最恰当的贝叶斯网.

做法: 定义评分函数(score function), 用来估计贝叶斯网与训练数据的契合程度, 再基于这个评分函数, 找出结构最优的贝叶斯网.

评分函数

将学习问题看成一个数据压缩任务, 目标是找到一个能以最短编码长度描述训练数据的模型, 编码的长度包括描述模型自身所需的字节长度和使用该模型描述数据所需的字节长度.

对于贝叶斯网学习而言, 模型就是一个贝叶斯网, 在训练过程中, 每个贝叶斯网描述了在训练数据上的概率分布, 最常出现的样本有最短的编码(与哈夫曼编码类似). 我们应该选择那个编码长度(包括模型和样本的编码)最短的贝叶斯网.

给定训练集 $D={x_1, x_2, \ldots, x_m}$, 贝叶斯网 $B=\langle G, \Theta \rangle$ 在 $D$ 上的评分函数可写为:

$$s(B \mid D) = f(\theta) \mid B \mid - LL(B \mid D)$$

其中, $\mid B \mid$ 是贝叶斯网的参数个数, $f(\theta)$ 表示描述每个参数 $\theta$ 所需的字节数, $LL(B \mid D) = \sum_{i=1}^{m}logP_B(x_i)$ 是贝叶斯网 $B$ 的对数似然.

$f(\theta) \mid B \mid$ 的意思是计算贝叶斯网 $B$ 所需的字节数.

$LL(B \mid D)$ 表示计算 $B$ 对应的概率分布 $P_B$ 需多少字节来描述 $D$.

于是, 学习任务就转化为一个优化任务, 寻找一个贝叶斯网 $B$, 使得评分函数 $s(B \mid D)$ 最小.

可以固定 $f(\theta)$, 使评分函数更加简单, 如这个值为 1 时表示每个参数用 1 字节描述, 可以得到 AIC 评分函数: $AIC(B \mid D) = \mid B \mid - LL(B \mid D)$.

贝叶斯网推理

在构造了贝叶斯网络之后, 我们可以利用贝叶斯网络来进行推理.

贝叶斯网络的推理, 是以其他变量的状态作为证据, 推理某些变量的状态. 这个推理的过程称为概率推理或信念更新.

已知的变量称为证据变量, 记为 $E$, 取值记为 $e$.

需要推理的变量称为查询变量, 记为 $Q$.

贝叶斯网络的概率推理算法有两种, 精确推理和近似推理. 这两种推理都是通过使用局部(边缘概率分布)的计算来避免计算的复杂程度(联合概率分布).

精确推理只适用于结点较少, 连接稀疏的网络.

近似推理降低了精度要求, 在有限时间内求得近似解.

近似推理

$\mathbf{Q}={Q_1, Q_2, \ldots, Q_n}$ 表示待查询变量.

$\mathbf{E}={E_1, E_2, \ldots, E_k}$ 表示证据变量, 取值为 $\mathbf{e}={e_1, e_2, \ldots, e_k}$.

我们的最终目标是计算后验概率 $P(\mathbf{Q}=\mathbf{q} \mid \mathbf{E}=e)$, 其中 $\mathbf{q}={q_1, q_2, \ldots, q_n}$ 是待查询变量的一组取值.

如书中所提的西瓜问题:

$\mathbf{Q}$={好瓜, 甜度}, $\mathbf{E}$={色泽, 敲声, 根蒂}, 且取值 $\mathbf{e}$={青绿, 浊响, 蜷缩}, 查询的目标值是 $\mathbf{q}$={是, 高}, 即这是好瓜, 且甜度高的概率有多大.

吉布斯采样

这是一种使用随机采样的方法, 完成贝叶斯网的近似推理.

吉布斯采样假设在第 $t$ 次采样中, $\mathbf{q}^t=\mathbf{q}^{t-1}$, 然后对非证据变量逐个进行采样, 改变其取值, 采样概率根据贝叶斯网 $B$ 和其他变量的当前取值 $\mathbf{Z}=z$ 计算获得. 假设经过 $T$ 次采样得到的与 $\mathbf{q}$ 一致的样本共有 $n_q$ 个, 则可近似估算出后验概率 $P(\mathbf{Q}=\mathbf{q} \mid \mathbf{E}=\mathbf{e}) \simeq \frac{n_q}{T}$.

可以看出, $t$ 时刻的状态只与 $t-1$ 时刻的状态有关, 因此, 这是一个马尔科夫链. 当 $t \rightarrow \infty$ 时, 必收敛.

不足点: 收敛速度慢, 需要很长时间才能趋于平稳; 如果贝叶斯网中存在极端概率 0 或 1, 则不能保证能平稳分布, 估计错误.

EM算法

在实际应用中, 训练样本中, 属性的值未必都是已知的, 如西瓜的根蒂脱落了, 则不能获悉其值是蜷缩还是硬挺. 像这种属性的变量值未知, 我们也称为未观测变量, 或隐变量.

令 $\mathbf{X}$ 表示已观测变量, $\mathbf{Z}$ 表示隐变量集, $\Theta$ 表示模型参数. 如果要对 $\Theta$ 做极大似然估计, 应该先最大化对数似然:

$$LL(\Theta \mid \mathbf{X}, \mathbf{Z}) = ln P(\mathbf{X}, \mathbf{Z}) \mid \Theta$$

但是 $\mathbf{Z}$ 是隐变量, 无法直接求解. 一种办法是对 $\mathbf{Z}$ 求期望, 来最大化已观测数据的对数"边际似然".

$$LL(\Theta \mid \mathbf{X}) = lnP(\mathbf{X} \mid \Theta) = ln \sum_{\mathbf{Z}}P(\mathbf{X}, \mathbf{Z} \mid \Theta)$$

EM 算法常用于估计参数隐变量. 如果属性间的依赖关系 $\Theta$ 已知, 则可以使用训练数据推断出最优隐变量 $\mathbf{Z}$, 若 $\mathbf{Z}$ 已知, 则可以对参数 $\Theta$ 做极大似然估计. 具体做法如下:

根据 $\Theta^{t}$ 推断隐变量 $\mathbf{Z}$ 的期望, 记为 $\mathbf{Z}^t$.
根据已观测变量 $\mathbf{X}$ 和 $\mathbf{Z}^t$ 对参数做极大似然估计, 记为 $\Theta^{t+1}$.

循环迭代上面两个步骤, 直到收敛.

如果不提取 $\mathbf{Z}$ 的期望, 可以通过 $\Theta^{t}$ 来计算 $\mathbf{Z}$ 的概率分布 $P(\mathbf{Z} \mid \mathbf{X}, \Theta^t)$, 步骤如下:

计算对数似然的期望值(E): $Q(\Theta \mid \Theta^t)=E_{\mathbf{Z} \mid \mathbf{X}, \Theta^t} LL(\Theta \mid \mathbf{X}, \mathbf{Z})$.
寻找参数最大化期望似然(M): $\Theta^{t+1}=arg max \limits_{\Theta} Q(\Theta \mid \Theta^t)$.

Pinvon's Blog

贝叶斯网

Table of Contents

概述

不确定性推理与联合概率分布

传统的使用概率方法进行不确定性推理

例子

条件独立与联合分布的分解

使用条件独立降低复杂度

贝叶斯网的概念

贝叶斯网的构造

确定网络结构

确定网络参数

图分隔与变量独立

概述

图分隔与变量独立

阻塞

马尔科夫边界与端正图

周志华-机器学习-贝叶斯网

例子

d-separation(有向分离)

贝叶斯网的学习

评分函数

贝叶斯网推理

近似推理

吉布斯采样

EM算法

Comments