密码学与安全技术
Table of Contents
Hash算法与数字摘要
Hash定义
Hash算法能将任意长度的二进制明文串映射为较短的二进制串, 并且不同的明文很难映射为相同的Hash值.
Hash值也称为指纹(fingerprint)或摘要(digest).
好的Hash算法能实现如下功能:
- 正向快速: 给定明文和Hashh算法, 能在有限时间内和有限资源内计算得到Hash值.
- 逆向困难: 给定Hash值, 在有限时间内很难逆推出明文.
- 输入敏感: 原始输入信息发生任何改变, 新产生的Hash值就出现很大的不同.
- 冲突避免: 很难找到两段内容不同的明文, 使得它们的Hash值一致(Hash一致也称为碰撞).
其中, "冲突避免"也称为"抗碰撞性", 如果给定明文的情况下, 无法找到与之碰撞的其他明文, 则算法具有"弱抗碰撞性"; 如果无法找到任意两个发生Hash碰撞的明文, 则称算法具有"强抗碰撞性".
即: 弱抗碰撞性: 给定明文 \(M\), 要找到另一个明文 \(M'\), 使得 \(H(M)=H(M')\) 很难. 强抗碰撞性: 找到两个随机明文 \(M\) 和 \(M'\), 使得 \(H(M)=H(M')\) 很难.
常见算法
MD4, MD5, SHA-1算法都被认为安全性已不足以应用于商业场景.
目前推荐至少使用SHA2-256, SHA-384, SHA-512或者更安全的算法. 且SHA-3相关算法也慢慢被提出来.
性能
一般对于Hash算法来说, 计算资源是瓶颈, 主频越高的CPU运行Hash算法的速度也越快, 可以通过硬件加速来提升Hash计算的吞吐量, 如采用FPGA来计算MD5值.
不过, 也有一些算法不是计算敏感型的, 如scrypt算法, 计算过程需要大量的内存资源, 节点不能简单增加更多CPU来获得Hash性能上的提升. 这种算法常用于避免算力攻击的场景.
数字摘要
数字摘要是Hash算法的一个重要用途. 利用Hash算法的抗碰撞性特点, 数字摘要可以解决确保内容未被篡改的问题.
如, 从网站下载文件, 有些网站会提供一个相应的数字摘要, 用户下载文件后, 可在本地计算文件的摘要, 与网站提供的摘要作对比, 从而检查文件内容是否被篡改.
Hash攻击与防护
Hash算法不是加密算法, 不能用于对信息的保护. 但Hash算法常用来保存用户密码, 这样即使数据库泄露, 也无法从Hash值还原密码.
关于攻击: 有些用户设置的密码过于简单, 有人专门搜集了这些常见密码, 计算对应的Hash值, 制作成字典. 这样通过Hash值可以快速反查到原始密码, 这一类型以空间换时间的攻击方法, 包括字典攻击和彩虹表(只保存一条Hash链的首尾值, 相对字典攻击, 可以节省存储空间)攻击.
关于防护: 一般在用户输入的密码基础上, 再加上一段随机字符串, 再计算合并后的字符串的Hash值. 将Hash结果和随机字符串分别存放在不同的地方, 只要不是两者同时泄露, 攻击者就很难破解了. 这种手段一般叫做: 加盐.
加解密算法
从设计理念上, 可以分为两大基本类型.
| 算法类型 | 特点 | 优势 | 劣势 | 代表算法 |
|---|---|---|---|---|
| 对称加密 | 加解密的密钥相同 | 计算效率高, 加密强度高 | 需提前共享密钥, 易泄露 | DES, 3DES, AES, IDEA |
| 非对称加密 | 加解密的密钥不相关 | 无需提前共享密钥 | 计算效率低, 仍存在中间人攻击可能 | RSA, ElGamal, 椭圆曲线系列算法 |
加解密系统基本组成
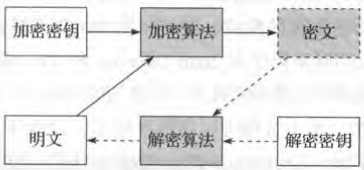
并非所有的加密算法的安全性都可以从数学上得到证明. 公认的高强度的加密算法和实现往往经过长时间各方面充分实践论证后, 才被大家所认可, 但也不代表其绝对不存在漏洞. 因此, 自行设计和发明未经过大规模验证的加密算法是一种不太明智的行为, 即使不公开算法加密过程, 也很容易被攻破, 无法在安全性上得到保障.
密码学实现的安全往往是通过算法所依赖的数学问题来提供, 而并非通过对算法的实现过程进行保密.
对称加密算法
对称密码从实现原理上可以分为两种: 分组密码和序列密码.
分组密码: 将明文切分成定长数据块, 作为基本加密单位.
序列算法: 每次只对一个字节或字符进行加密处理, 且密码不断变化.
对称密码的主要问题有两个: 一是各参与方都要提前持有密钥, 一旦有人泄露则安全性被破坏; 二是如何在不安全通道中提前分发密钥, 需要借助Diffie-Hellman协议或非对称加密方式来实现.
非对称加密算法
私钥一般通过随机数算法生成, 公钥可以根据私钥生成. 公钥公开, 私钥自己保管.
非对称加密算法的安全性往往需要基于数学问题来保障, 目前主要有基于大数质因子分解(RSA), 离散对数, 椭圆曲线等经典数学难题进行保护.
RSA类算法可能在不远的将来被破解, 如果可以, 更推荐采用高安全强度的椭圆曲线系列算法.
选择明文攻击
由于公钥可以获取, 因此任何人都可以给定明文, 获取对应的密文.
为了规避这种风险, 现有的非对称加密算法都引入了一定的保护机制, 对同样的明文使用同样密钥进行多次加密, 得到的结果完全不同, 这就避免了选择明文攻击的破坏.
如何实现: 可以先对明文进行变形, 如添加随机的字符串或标记, 再对结果进行处理; 也可以先用随机生成的临时密钥对明文进行对称加密, 然后再对对称密钥进行加密, 即混合利用多种加密机制.
混合加密机制
先用计算复杂度高的非对称加密协商出一个临时的对称加密密钥(也称为会话密钥), 然后双方再通过对称加密算法对传递的大量数据进行快速的加解密处理. 如HTTPS协议.
HTTPS在传统的应用层和传输层之间引入TLS/SSL加密层来实现可靠的传输.
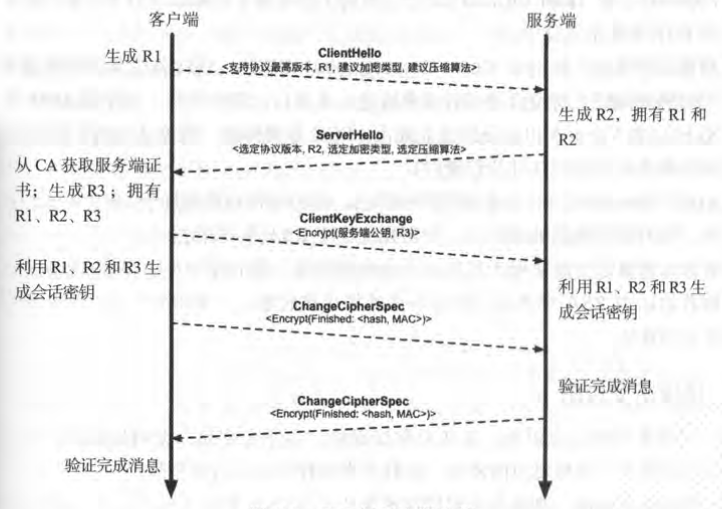
Figure 2: TLS握手协商过程
- 浏览器发送信息到服务器, 包括随机数R1, 支持的加解密算法类型, 协议版本, 压缩算法等, 该过程为明文.
- 服务器返回信息, 包括随机数R2, 选定加密算法类型, 协议版本和服务器证书, 该过程为明文.
- 浏览器检查带有服务器公钥的证书. 证书要由第三方CA来签发, 浏览器和OS会预置权威CA的根证书. 如果证书被篡改或造假, 很容易通过CA的证书验证出来.
- 如果证书没问题, 浏览器用服务器证书中的公钥加密随机数R3(也叫Pre-MasterSecret), 发送给服务器. 此时, 浏览器和服务器都拥有R1, R2, R3信息, 基于随机数R1, R2, R3, 双方通过伪随机数函数来生成共同的对称会话密钥MasterSecret.
- 后续浏览器和服务器的通信都通过对称加密算法(如AES)进行保护.
消息认证码与数字签名
消息认证码和数字签名技术, 通过对消息的摘要进行加密, 可用于消息防篡改和身份证明问题.
消息认证码
消息认证码全称基于Hash的消息认证码(Hash-based Message Authentication Code), 基于对称加密, 可用于对消息完整性进行保护.
过程: 对某个消息利用提前共享的对称密钥和Hash算法进行加密处理, 得到HMAC值. HMAC值持有方可以证明自己拥有共享的对称密钥, 并且也可以利用HMAC确保消息内容未篡改.
HMAC算法包括三个参数, 提前共享的对称密钥K, 提前商定的Hash算法H, 要处理的消息内容M.
使用场景: A和B提前共享HMCA的密钥和Hash算法. A需要确认对方是否为B, 可发送随机消息给B. B收到消息后进行计算, 把消息HMAC值返回给A, A通过检验HMAC值的正确性, 可以确认对方是否为B.
消息认证码使用过程中主要问题是需要共享密钥, 如果密钥被多方拥有, 无法证明消息来自某个确切的身份. 这种情况下, 使用非对称加密方式, 可以追溯到来源身份, 即数字签名.
数字签名
数字签名基于非对称加密, 既可以用于证实数字内容的完整性, 又可以确认来源(不可抵赖).
使用场景: A给B发送一个文件, B如何确认这就是A发出的原始版本? A可以先对文件内容进行摘要, 然后用自己的私钥对摘要进行加密(签名), 之后同时将文件和签名都发给B. B收到文件和签名后, 用A的公钥来解密签名, 得到数字摘要, 与收到文件进行摘要后的结果进行比对, 如果一致, 说明文件确实是A发送的, 且内容未被修改.
数字签名算法有DSA, ECSDA等.
除了普通的数字签名应用场景外, 还有一些特殊的数字签名技术:
- 盲签名: 签名者需要在无法看到原始内容的前提下对信息进行签名. 盲签名可以实现对所签名内容的保护, 防止签名者看到原始内容; 盲签名可以实现防止追踪, 签名者无法将签名内容和签名结果进行对应.
- 多重签名
- 群签名: 即某个群组内一个成员可以代表群组进行匿名签名, 签名可以验证来自于该群组, 但无法准确追踪到签名的是哪个成员.
- 环签名: 一种简化的群签名.
数字证书
对于非对称加密算法和数字签名来说, 很重要的一点就是公钥的分发. 理论上任何人都可以公开获取到对方的公钥.
但是这个公钥有没有可能被伪造呢? 传输过程中有没有可能被篡改?
如果公钥出现了问题, 则整个建立在其上的安全体系将崩溃.
数字证书就是为了解决这个问题. 它就像现实生活中的证书一样, 可以证明所记录信息的合法性.
根据所保护的公钥的用途, 数字证书可以分为加密数字证书和签名验证数字证书.
加密数字证书保护用于加密信息的公钥.
签名验证数字证书保护进行解密签名, 进行身份验证的公钥.
这两种类型的公钥可以同时放在同一证书中.
证书需要由权威的CA进行签发和背书, 如果是私有网络, 也可以自己搭建本地CA系统.
X.509证书规范
数字证书的内容主要有: 基本数据(版本, 序列号), 所签名对象信息(签名算法类型, 签发者信息, 有效期, 被签发人, 签发的公开密钥), CA的数字签名.
目前证书的内容广泛使用X.509规范.
证书格式
X.509规范中, 一般推荐使用PEM格式来存储证书相关的文件. PEM格式采用文本方式进行存储, 一般包括首尾标记块和内容块, 内容块采用base64进行编码.
可以使用 openssl 工具来查看PEM文件的内容.
openssl x509 -in xxx.pem -noout -text
如图所示:
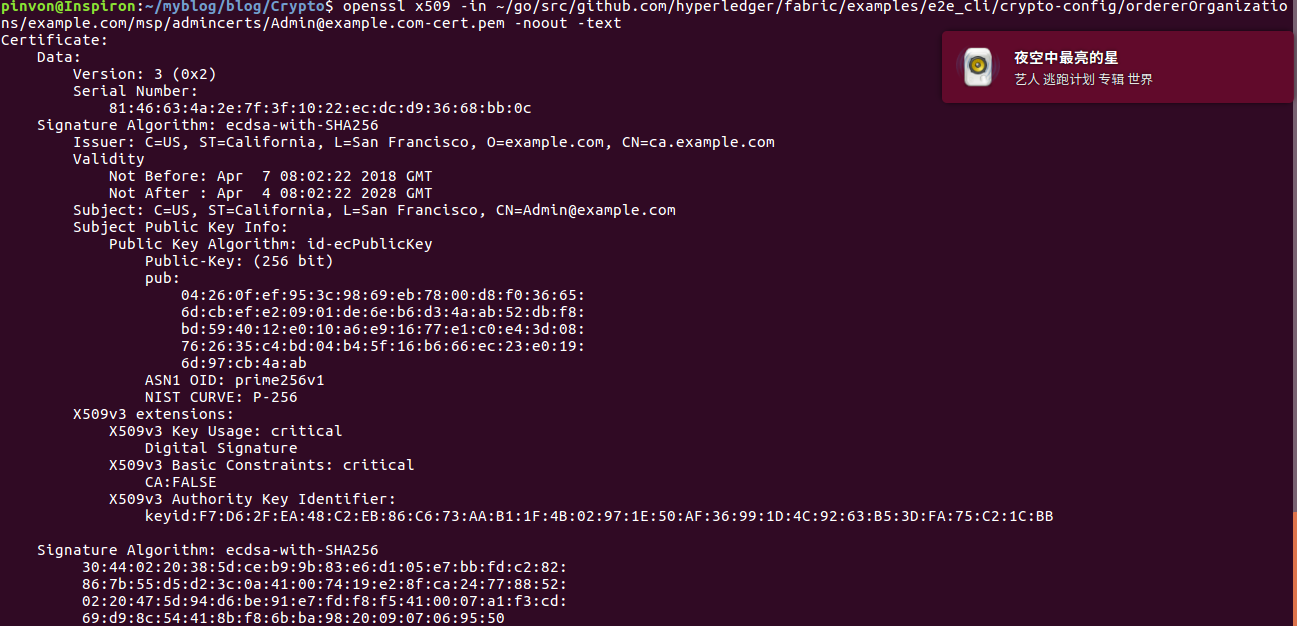
证书信任链
证书中记录了大量的信息, 其中最重要的是"签发的公钥"和"CA数字签名"两个信息.
只要使用CA的公钥再次对这个证书进行签名, 然后比对, 就能证明某个实体的公钥是否合法. 如果"签发的公钥"被篡改过, 比对的结果肯定不同.
那么, 如何证明CA的公钥是否合法, 是否被篡改?
关于CA自身的合法性: 可以通过更上层的CA颁发的证书来进行认证; 也可以通过预先颁发的根CA来实现信任基础. 目前, 主流的OS和浏览器里, 都会提前预置一些权威CA的证书(通过CA自身的私钥签名, 系统承认这些是合法的证书). 之后所有基于这些CA认证过的中间层CA(Intermediate CA)和后继CA都会被验证合法.
PKI体系
PKI体系提供了一套完整的证书管理框架, 包括生成, 颁发, 撤销等.
在非对称加密中, 公钥可以通过证书机制来进行保护, 但证书的生成, 分发, 撤销等过程未在X.509规范中进行定义.
PKI基本组件
CA: 负责证书的颁发和作废, 接收来自RA的请求
RA: 对用户身份进行验证, 检验数据合法性, 负责登记, 审核过了就发给CA
证书数据库: 存放证书
流程: 用户通过RA登记申请证书, 提供身份和认证信息等, CA审核后完成证书的制造, 颁发给用户; 用户如果需要撤销证书, 需要再次向CA发出申请.
证书的签发
CA对用户签发证书, 实际上是对某个用户的公钥, 使用CA的私钥对其进行签名. 这样任何人都可以用CA的公钥对该证书进行合法性验证. 验证成功则认可该证书中所提供的用户公钥内容, 实现用户公钥的安全分发.
用户证书的签发有两种方式: 一种是由CA直接生成证书(内含公钥), 将证书和对应的私钥发给用户; 另一种是由用户自己生成公钥和私钥, 由CA来对公钥进行签名.
对于第二种情况, 用户要自行生成一个私钥和证书申请文件(CSR), 该文件中包含了用户对应的公钥和一些基本信息. CA只需要对证书请求文件进行签名, 生成证书文件, 颁发给用户即可. 这种方式中, 用户可以保持私钥信息的私密性, 不会被其他方获知(包括CA方). 但是这种情况下, 如果用户的私钥丢失, 由于CA不持有私钥信息, 无法进行恢复.
证书申请文件的生成:
openssl req -new -keyout private.key -out for_request.csr
生成的过程中需要输入地理位置, 组织, 通用名等信息, 生成的私钥和csr文件, 默认以PEM格式存储.
证书的撤销
证书超出有效期后会作废, 用户可以主动向CA申请撤销某证书文件.
由于CA无法强制收回已经颁发的证书, 所以还要维护一个撤销证书列表, 用户记录已经撤销的证书序号.
Generated by Emacs 25.x(Org mode 8.x)
Copyright © 2014 - pinvon - Powered by EGO
